Self-testing QRNG

Description

La génération de nombres aléatoires joue un rôle crucial dans de nombreuses applications scientifiques et technologiques, en particulier pour la simulation et la cryptographie. Il est d'une importance fondamentale que les nombres générés soient vraiment aléatoires, car toute déviation peut compromettre la sécurité. Notamment, les violations récentes des protocoles cryptographiques ont exploité les faiblesses de la génération de nombres aléatoires. Dans ce contexte, les procédés exploitant le caractère aléatoire inhérent de la physique quantique ont été largement étudiés. Les dispositifs de génération de nombres aléatoires quantiques (QRNG) sont maintenant disponibles dans le commerce, ce qui représente sans doute l'un des développements les plus réussis des technologies quantiques à ce jour.

Malgré ce succès, des développements récents ont mis en évidence une faiblesse générale et une limitation des dispositifs QRNG standards (y compris tous les dispositifs commerciaux). Spécifiquement, ces dispositifs ne fournissent pas une indication précise de l'entropie, soit la qualité du caractère aléatoire des informations générées. Cela a été reconnu comme un problème crucial pour les générateurs QRNG. En pratique, il est généralement difficile d'estimer avec précision l'entropie, car tout dispositif est sujette à des imperfections techniques inévitables qui conduisent à un bruit. Il est aussi possible que les performances d'un dispositif QRNG se dégrade avec le temps. Il est possible qu'à un instant donné la qualité des nombres aléatoires soit fortement diminuée sans que l'utilisateur en soit conscient.

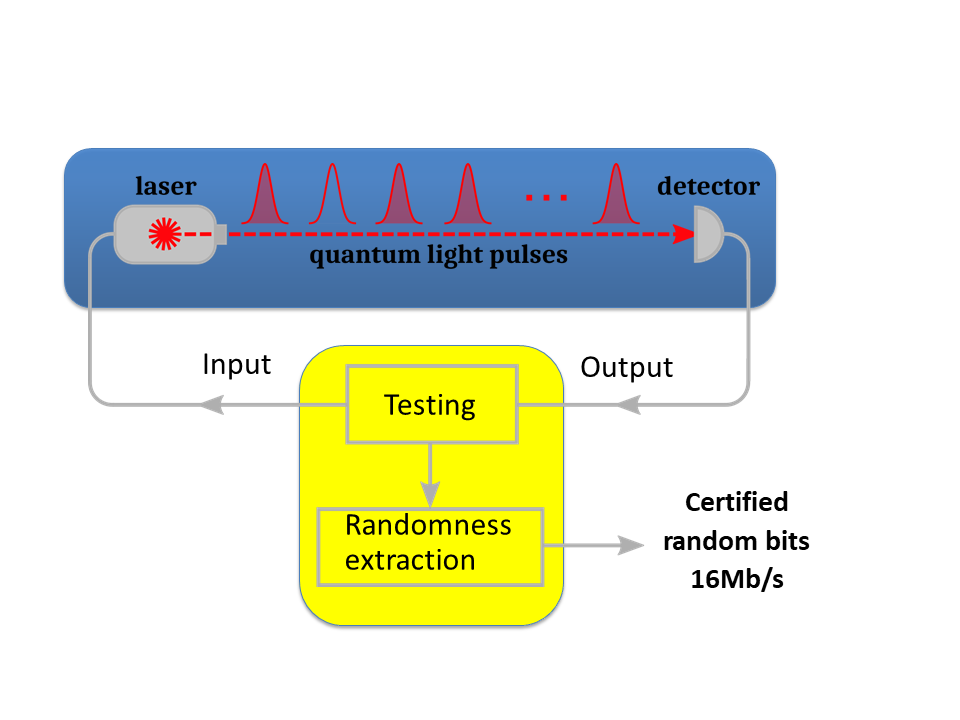
Le groupe GAP de l'UNI-GE a proposé récemment une solution prometteuse pour résoudre les problèmes ci-dessus, en développant un système QRNG «auto-testé». Le dispositif QRNG effectue en permanence un test afin de certifier en continu si la génération des nombres est vraiment aléatoires. Spécifiquement, le générateur quantifie la quantité d'entropie quantique générée par le système en temps réel. Ce procédé combine une forte sécurité et une facilité de mise en œuvre, comme nous l'avons démontré dans une expérience de démonstration du principe, en obtenant des taux de génération aléatoires comparables aux QRNG commerciaux (~ 10 MHz). L'objectif principal du présent projet est de développer un démonstrateur pour un générateur QRNG auto-testé. Celui-ci devra être compact, simple à utiliser et atteindre des débits élevés. Surtout, il devrait comprendre uniquement des composants optiques et électroniques standard, afin d'assurer un faible coût. Ce démonstrateur permettra de combler le fossé entre les algorithmes de traitement de l'information quantique, qui sont abstraits et indépendants du dispositif, et la technologie quantique commerciale.

La figure ci-dessous montre le fonctionnement général du dispositif.

Le challenge du projet pour l'équipe du REDS fut de réaliser l'extraction des bits aléatoires (random bits). Il s'agit de calculer l'extraction des bits aléatoires à l'aide d'une matrice de Toeplitz sur un très grand nombre de bits pseudo aléatoire reçu par le détecteur de photon (raw bits). L'entropie du système augmente avec la taille du nombre de raw bits qui sont traité avec la matrice. La figure ci-dessous vous présente la structure du calcul de l'extraction à l'aide de la matrice de Toeplitz.

Après plusieurs recherches il est apparu que l'utilisation d'un CPU ou DSP ne permettrait pas d'obtenir une grande taille de matrice avec un calcul en temps réel. Actuellement les raw bits ont un débit de 50 Mbits/sec. Nous avons alors développé un design numérique pour une intégration dans une FPGA à prix acceptable. Nous avons été confronté à plusieurs difficultés. L'intégration directe de la matrice donnait de très mauvais résultats. Nous avons donc décomposé le calcul selon la solution proposé dans un article IEEE de 2016 [1]. Les performance étaient meilleur, mais encore largement en dessous de la taille souhaitée. Nous avons alors décomposé la matrice en petite sous-matrice qui sont réutilisées plusieurs fois.

Voici une vue générale de la décomposition de la matrice de Toeplitz.

En parallèle, nous avons développé un design qui permet de déterminer en temps réel le taux d'entropie du paquets de bits raw qui est traité par la matrice. Nous délivrons les bits random seulement si l'entropie de ceux-ci est garantie. Le taux actuel de l'entropie du système optique développé par le GAP est d'environ 20 %.

Les résultats obtenus pour l'extraction des bits aléatoires avec la matrice de Toeplitz dans une FPGA Artix7 de Xilinx sont les suivants :

• Taille de la matrice de Toeplitz : 1'500'000 x 300'000
• Entropie de l'optique : 20 %
• Extraction sur un paquet de 1'500'000 bits raw pour obtenir 300'000 random bits

Finalement l'ensemble du dispositif a été intégré dans un boîtier. L'équipe de l'institut REDS a développé une carte embarquée comprenant un microcontrôleur et la FPGA ainsi que les différentes interfaces pour interfacer les composants optique.

Voici le schéma bloc du système réalisé:

Finalement l'ensemble est intégré dans un boîtier compact. Celui-ci peut-être connecté à un PC via une ligne Ethernet afin de piloter le système et récupérer les bits random.

[1] IEEE FPGA Implementation of Toeplitz Hashing Extractor for Real Time Post-processing of Raw Random Numbers; Xiaoguang Zhang, You-Qi Nie, Hao Liang, Jun Zhang

Partenaires